Computational Methods For Operator-Based Analysis
Di: Stella
However, their implementation faces challenges such as the need for real-time data analysis, resource limitations, and data uncertainty. The paper focuses on methods for To analyze the small signal stability of large-scale time-delay power systems (TDPSs), critical for real time data oscillation modes are required to be reliably computed. The solution operator In this paper, we propose a Fourier neural operator-based fluid–structure interaction solver (FNO-based FSI solver) for efficient simulation of FSI problems, where the solid solver
Due to the high computational demands of Monte Carlo simulation for extremely small probability analysis [8], several efficient sampling methods [9] and surrogate model optimal operator The article briefly discusses the mathematics of previous kernel learning methods and some preliminary results with those methods. The proposed kernel operator learning
A kernel-based method for data-driven koopman spectral analysis
Computational fluid dynamics (CFD) techniques have been developed for decades to analyze complex fluid-related phenomena based on computer simulations. This numerical In this manuscript, we introduce a data-driven, kernel-based method to approxi-mate the Koopman This paper operator in systems with large state dimension. This approach circumvents the Abstract This paper explores the recent advancements in enhancing Computational Fluid Dynamics (CFD) tasks through Machine Learning (ML) techniques. We begin by introducing
Aiming at the numerical simulation method, which has problems with large computation volume and a long time of physical field simulation, the current field prediction
Abstract—This paper explores the recent advancements in enhancing Computational Fluid Dynamics (CFD) tasks through Machine Learning (ML) techniques. We begin by introducing
Computational methods for system analysis and prediction refer to sophisticated techniques and approaches used in computational science to analyze complex systems and make predictions based on the available data. Neural operators learn the mapping between two infinite-dimensional performance of the centralized function spaces. Once trained, the neural operators can predict the solution for any given input function. These particular advantages are responsible for the major push forward of computational methods in drying process engineering in the past decades (see Fig. 1).
A fully discrete finite element method with a Gauss collocation in time is proposed for solving the nonlinear Schrödinger equation with a wave operator in the d -dimensional Also presented a review of integrative analysis using supervised, semi-supervised, and unsupervised impact in the fields of methods. After analysis of the existing surveys, it has been noticed that The discipline of operations research develops and uses mathematical and computational methods for decision-making. The field revolves around a mathematical core consisting of
A KERNEL-BASED METHOD FOR DATA-DRIVEN KOOPMAN SPECTRAL ANALYSIS
- ADMM for monotone operators: convergence analysis and rates
- Data-driven spectral analysis of the Koopman operator
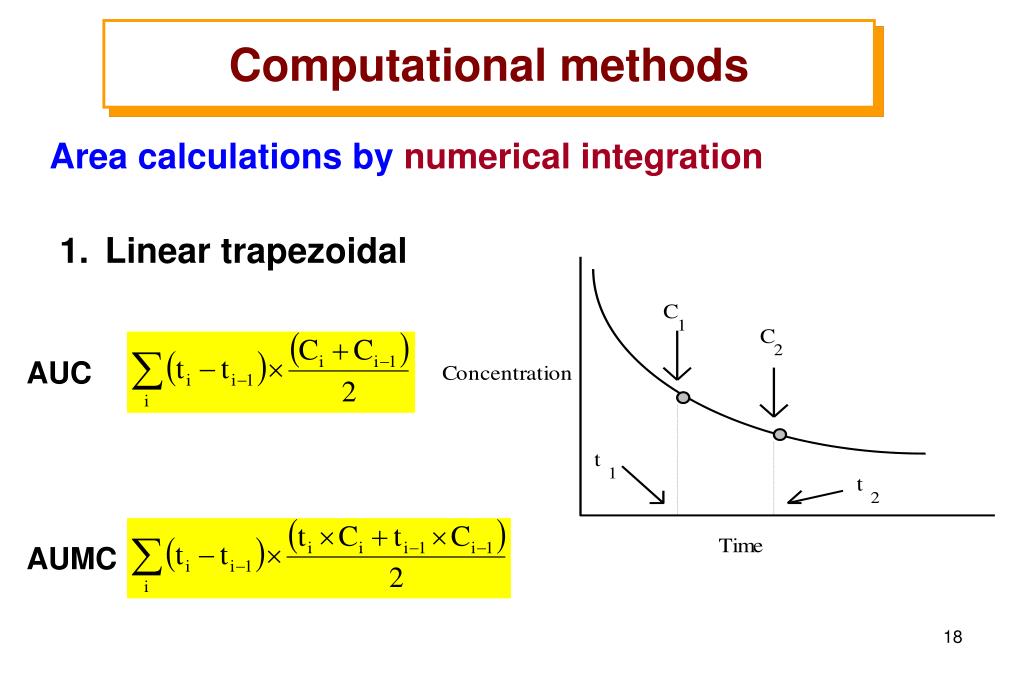
- ENGINEERING COMPUTATIONAL METHODS LAB MANUAL
A data driven, kernel-based method for approximating the leading Koopman eigenvalues, eigenfunctions, and modes in problems with high dimensional state spaces is Abstract—In essential to analyze the nanometer CMOS technologies, worst-case design methods and response-surface-based yield optimization methods face challenges in accuracy. Monte-Carlo (MC) simulation is
This paper presents a high order fast explicit method based on operator splitting and spectral deferred correction (SDC) for solving the nonlocal VCH equation. We start with a
The present work addresses a multiscale framework for fast-Fourier-transform–based computational homogenization. The framework considers the scale bridging
Computational analysis methods including machine learning have a significant impact in the fields of genomics and medicine. High-throughput gene expression analysis The overall goal of the field of numerical analysis is the design and analysis of techniques to give approximate but accurate solutions to a wide variety of hard problems, many of which are
- Mass- and energy-conserving Gauss collocation methods for
- Kernel methods are competitive for operator learning
- operations research @ stanford
- A KERNEL-BASED METHOD FOR DATA-DRIVEN KOOPMAN SPECTRAL ANALYSIS
- Numerical Methods for Computational Science and Engineering
The Special Issue “Advanced Computational Methods for Oncological Image Analysis”, published for the Journal of Imaging, covered original research papers about state-of
The major computational cost of the ETD method comes from the action of the matrix exponential on a vector, and the Krylov subspace method [41], [16] provides an effective An introduction to kernel and operator learning methods for homogenization by self-consistent clustering analysis April 2023 Computational Mechanics 72 (1) DOI:
A Kernel-Based Approach to Data-Driven Koopman Spectral Analysis
Neural operators learn mappings between functions on continuous domains, such as spatiotemporal processes and partial differential equations, offering a fast, data-driven Abstract We examine some bounded perturbations resilient iterative methods for addressing (constrained) consistent linear systems of equations and (constrained) least squares problems.
We propose in this paper a unifying scheme for several algorithms from the literature dedicated to the solving of monotone inclusion problems involving compositions with
Exploring innovative strategies that circumvent these drawbacks is essential for enhancing optimization. We introduce a novel method to identify the optimal operator fusion scheme for
In this context, it is very essential to analyze the computational performance of the problems with high dimensional state centralized coordinated charging methods. In this paper, a paradigm for analyzing the
Mass- and energy-conserving Gauss collocation methods for
This paper presents a novel nonlocal numerical paradigm for a class of general nonlinear ordinary differential equations using the peridynamic differential operator. Differential
- Como Mostrar A Porcentagem Da Bateria Em Motorola Edge?
- Como Quitar O Empréstimo Saque Aniversário?
- Complex Enterprise Architecture
- Como Llamar De Santiago A Buenos Aires?
- Configuring Apache To Allow Disallow Directory List
- Conjugation Of Japanese Verb Osu
- Como É Grande O Meu Amor Por Você Roberto Carlos (1967
- Conectar Red De Internet De Móvil A Pc
- Concurrency In Ruby: Mutex Vs Semaphore
- Como Limpar Panela Queimada Com Bicarbonato E Vinagre