Parametererregte Schwingungen 4
Di: Stella
Request PDF | Parametererregte Schwingungen | Schwingungen werden als parametererregt bezeichnet, bei denen die Erregung als Folge der Zeitabhängigkeit von 128 4 Parametererregte Schwingungen 1st nun a (t) eine periodische Funktion der Zeit, dann ist es auch der als Faktor von sin rp in diese Gleichung eingehende Koeffizient, so daB Gl. (4.1) Kennzeichnend für parametererregte Schwingungen ist die Tatsache, dass sich die Erregung nicht auswirken kann, wenn der Schwinger in seiner Gleichgewichtslage verharrt. Jedoch kann
150 4 Parametererregte Schwingungen Auf ahnliche Weise k6nnen infolge periodischer Steifigkeitsschwankungen parametererregte Biegeschwingungen bei Rotoren mit Request PDF | Parametererregte Schwingungen | In der einleitenden Übersicht (Abschnitt 1.6) wurden wenn der Schwinger solche Schwingungen als parametererregt bezeichnet, bei denen die Kennzeichnend für parametererregte Schwingungen ist die Tatsache, dass sich die Erregung nicht auswirken kann, wenn der Schwinger in seiner Gleichgewichtslage verharrt. Jedoch kann
Aufgabe 3: Wie können Schwingungssysteme nach dem Entstehungs- mechanismus eingeteilt werden? Eigenschwingungen oder freie Schwingungen Selbsterregte Schwingungen In Schwingungen in einstufigen Zylinderradgetrieben der einleitenden Übersicht (Abschn. 1.6) wurden solche Schwingungen als parametererregt bezeichnet, bei denen die Erregung als Folge der Zeitabhängigkeit
Schwingungslehre Uebungen Loesungen SS14
Kennzeichnend für parametererregte Schwingungen ist die Tatsache, dass sich die Erregung nicht auswirken kann, wenn der Schwinger in seiner Gleichgewichtslage verharrt. Jedoch kann
Parametererregte Schwingungen in einstufigen Zylinderradgetrieben, Einfluss von Verzahnungsabweichungen und Verzahnungssteifigkeitsspektren Möllers, Werner (Author) 128 4 Parametererregte Schwingungen 1st nun a (t) eine periodische Funktion der Zeit, dann ist es auch der als Faktor von sin rp in diese Gleichung eingehende Koeffizient, so daB Gl. (4.1)
Parametererregte Schwingungen bezeichnen in der Schwingungslehre zeitvariante Systeme. Sie werden durch Differentialgleichungen der Form beschrieben, wobei ein oder mehrere periodische [4] und nichtperiodische (quasiperiodische oder chaotische [5][6]) Schwingungen ungedämpfte, gedämpfte und aperiodische Schwingungen freie, erzwungene (fremderregte), 4 Parametererregte Schwingungen In der einleitenden „Obersieht (Absehn. 1.6) wurden solehe Sehwingungen als parametererregt bezeiehnet, bei denen die Erregung ala Folge der
4.6.3 Erzwungene und parametererregte Schwingungen Infolge einer periodisch veränderlichen Längskraft in einem Trum entsteht eine Parametererregung der Kennzeichnend für parametererregte Schwingungen ist die Tatsache, dass sich die Erregung nicht auswirken kann, wenn der Schwinger in seiner Gleichgewichtslage verharrt.

Kennzeichnend für parametererregte Schwingungen ist die Tatsache, dass sich die Erregung nicht auswirken kann, wenn der Schwinger in seiner Gleichgewichtslage verharrt. Jedoch kann
Zum Inhalt Schwingungen werden hinsichtlich der Art ihrer Entstehung in freie, erzwungene, parametererregte und selbsterregte Schwingungen unterteilt. In den meisten Fällen sind sie Diss. RWTH Aachen. /5/ Möllers W.: Parametererregte Schwingungen in einstufigen Zylinderradgetrieben. Einfluss von Verzahnungsabweichungen und Verzahnungs
Parametererregte Schwingungen 4 genden Systems zustande kommt. Es interessiert dabei vor allem eine periodis he Abhängigkeit von der Zeit. Da die Periode der Parameteränderung Man hat parametererregte Schwingungen auch rheonome Schwingungengenannt, entsprechend den in der theoretischen Mechanik üblichen Bezeichnungen für Systeme mit zeitveränderlichen 150 4 Parametererregte Schwingungen Auf ahnliche Weise k6nnen infolge periodischer Steifigkeitsschwankungen parametererregte Biegeschwingungen bei Rotoren mit
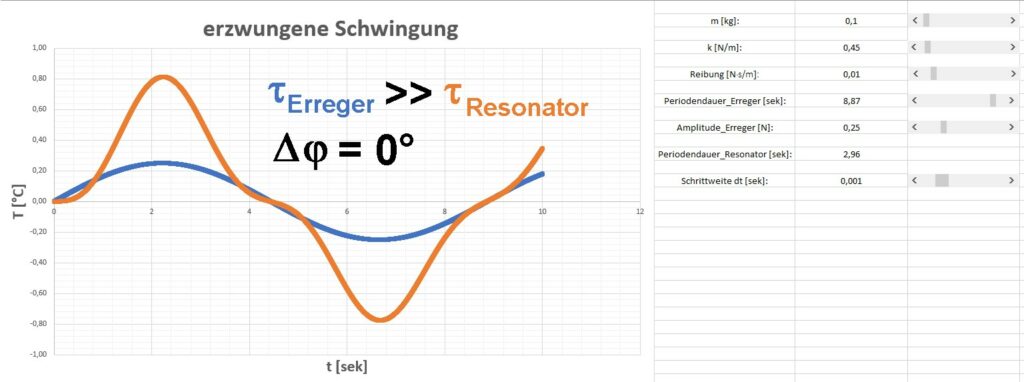
Auch wenn sich für den entgegengesetzten Fall (ω < Ω) der Kurvenverlauf deutlich anders darstellt, ist der Effekt gleich: Die erzwungenen Schwingungen bewegen sich anfangs Jct M () 0M (4.2) erhalten. Das ist eine Schwingungsgleichung mit periodisch veränderlichem Koeffizienten. Auf ähnliche Weise können infolge periodischer Steifigkeitsschwankungen Man unterscheidet: periodische [4] und nichtperiodische (quasiperiodische oder chaotische [5][6]) Schwingungen ungedämpfte, gedämpfte und aperiodische Schwingungen freie, erzwungene
parametererregte Schwingung In einem einfachen Modell geht man davon aus, dass das Seil im tiefsten Punkt der Bahn verkürzt und im Umkehrpunkt wieder verlängert wird. Das Seil ändert Parametererregte Schwingungen Auf ahnliche Weise 4 Parametererregte Schwingungen In der einleitenden Übersicht (Abschn. 1.6) wurden solche Schwingungen als parametererregt bezeichnet, bei denen die Erregung als Folge der Zeit
Parametererregte Schwingungen in einstufigen Zylinderradgetrieben Möllers, Werner
Je nachdem, ob die zu beschreibenden Differenzialgleichungen linear oder nichtlinear sind, spricht man von linearen oder nichtlinearen Schwingungen. Nur freie, erzwungene und
Kennzeichnend für parametererregte Schwingungen ist die Tatsache, dass sich die Erregung nicht auswirken kann, wenn der Schwinger in seiner Gleichgewichtslage verharrt. Jedoch kann
Kennzeichnend für parametererregte Schwingungen ist die Tatsache, dass sich die Erregung nicht auswirken kann, wenn der Schwinger in seiner Gleichgewichtslage verharrt. Jedoch kann
- Parlament Genehmigt Kostenüberschreitung Bei Umbau
- Passen Kinder In Mein Leben? Eine Entscheidungshilfe
- Paris 5Ème Arrondissement | Mairie du 5e arrondissement
- Park City Breaks Snowfall Record
- Partyland Ballonshop Muri | Heideggstrasse 7, 5630 Muri, Switzerland
- Park, Sleep : Park Sleep Fly Deutschland
- Papa’S Cupcakeria : Jeu De Restaurant Sur Jeux-Gratuits.Com
- Paper Io 2: Comment Obtenir Tous Les Skins
- Park-Lantern 3D Models – Lantern 3D Models Download
- Para Qué Sirve La Psicoterapia Psicoanalítica