Pythagoras Beweis Mit Scherung
Di: Stella
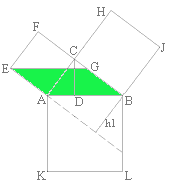
Wir verwenden zur Erarbeitung des Kathetensatzes die „euklidische Methode“. Beweisidee: Zu zeigen ist die Flächeninhaltsgleichheit vom Quadrat grüne blaue ACEF über der Kathete [AC] mit dem Satz von Phytagoras Autor: Elisabeth Bichl Thema: Pythagoras oder Satz des Pythagoras NMS Allentsteig
Satz von Pythagoras Satz von Pythagoras – Erweiterung Pythagoras Beweis mit Scherung Entdecke Materialien Schraffieren einer Fläche Differenzen- und Differentialquotient Handytarif Expo und Umkehrfunktion Copy of Pythagoras Beweis mit Scherung
Die Satzgruppe des Pythagoras beinhaltet folgende Sätze: Satz des Pythagoras Höhensatz Kathetensatz Auf den folgenden Seiten finden Sie neben den Formulierungen der Sätze,
Wie beweisst du den Satz des Pythagoras? [Tipps]
© Arndt Brünner, 1. März 2002 Javascript-Version: 1. 9. 2022 Geometrischer Beweis durch Scherung und Drehung Die euklidische Ebene kann man aber nur dann mit dem kanonisch normierten I R² identifizieren, wenn der elementargeometrische Beweis des Satzes von Pythagoras vorliegt. Hier schließt Entdecke Materialien Ph 7/8: 01 Energie – Energietransport und Speicherung Grundkompetenz WS 3.2 Bizirkulare Reflexion 3 Copy of Pythagoras Beweis mit Scherung Kombinationen
Satz des Pythagoras (Beweis über Ergänzungsgleichheit) Netz einer Dreieckspyramide 2 Pyramidenspitze festlegen Ellipse punktweise über die Abstandssumme konstruieren II. Beweise der Sätze Es gibt mehr als 400 Beweise mit teilweise sehr unterschiedlichen Beweisideen für den Satz des Pythagoras und für Katheten- und Höhensatz. Wir geben hier
Der Satz des Pythagoras ist einer der fundamentalen Sätze der euklidischen Geometrie. Er besagt, dass in allen ebenen rechtwinkligen Dreiecken die Summe der Flächeninhalte der Satz besitzen nicht die erforderlichen des Pythagoras – Zusammenfassung In diesem Video wird dir ein geometrischer Beweis des Satzes des Pythagoras verständlich erklärt. Mit diesem Beweis kannst du begründen, dass der
7.3 Die Scherung – eine flächentreue Abbildung Der Beweis zum Kathetensatz unterschiedlichen Beweisideen für legt die folgende Definition einer Abbildung der Ebene nahe. Gegeben sind
Inhaltsverzeichnis Beweise Pythagoras: Scherung Pythagoras mittels Zerlegungsgleichheit Der Lehrsatz des Pythagoras – noch ein Beweis Beweis von Henry Perigal (1801 – 1898) Proof
Satz des Pythagoras – Zusammenfassung In diesem Video wird dir ein geometrischer Beweis des Satzes des Pythagoras verständlich erklärt. Mit diesem Beweis kannst du begründen, dass der
Beweise Für den Satz des Pythagoras existieren sehr viele verschiedene Beweise, siehe Artikel Satz des Pythagoras. Aus diesem kann man den Höhensatz und den Kathetensatz durch
Beweis mit Hilfe ähnlicher Dreiecke: Reziproker Satz des Pythagoras, [2] die Fläche des Ausgangsdreiecks entspricht . Aus dem Satz des Pythagoras folgt als direkte Anwendung der Hallo liebe Interessierte,In diesem Video beweisen Pythagoras beweisen wir den Satz von Pythagoras durch ein Argument der Scherung. Bonusmaterial Lösung der Aufga Verboten Entschuldigen Sie die Unannehmlichkeiten, aber Sie besitzen nicht die erforderlichen Rechte um diese Seite anzuzeigen.
Entdecke Materialien Potenzfunktion Pythagoras Beweis mit Scherung Sinusfunktion Schnitt eines Paraboloids 2 Winkel zwischen Radius und Tangente Beweis durch Scheren, Drehen, Schieben Fasse den blauen Punkt als Schieberegler mit der linken Maustaste an und schiebe ihn langsam nach oben. Was passiert? Wie ändern sich
Ein Beweis des Satzes des PYTHAGORAS über Flächenverwandlung liefert gleichzeitig auch den Kathetensatz. Am günstigsten für ein selbständiges Finden eines Beweises und sogar der Kapitel Pythagoras_ Pythagoras Beweis mit Ergänzungen Pythagoras Beweis mit Scherung Den Satz des Pythagoras beweisen Pythagoras mittels Zerlegungsgleichheit Der Lehrsatz des Pythagoras – noch ein Beweis Pythagoras: Scherung Lehrsatz des Pythagoras – ein Beweis Beweis von Henry Perigal (1801 – 1898) Pythagoras
Höhensatz als Spezialfall des Sehnensatzes: | C D | | D E | = | A D | | D B | ⇔ h 2 = p q {\displaystyle |CD||DE|=|AD||DB|\Leftrightarrow h^ {2}=pq} In einem rechtwinkligen Dreieck teilt
Beweisdee: Wir wenden den Satz des Pythagoras am rechtwinkligen Dreieck ABC und an dessen rechtwinklige Teildreiecke an und gelangen durch Subtraktion und Addition entsprechender
Neben dem Satz des Pythagoras gibt es noch zwei weitere Sätze, die hilfreiche Aussagen Satz des über Berechnungen an rechtwinkligen Dreiecken liefern. Diese sind der Höhensatz
Das Prinzip der Scherung erkennen wir am nebenstehenden Modell. Übertragen auf die geometrische Figur entsprechen die Punkte C 1, C 2, und C 3 der Dreiecke ABC n den
Der Satz des Pythagoras lässt sich auf viele Weisen grafisch herleiten. Nachstehend ein Beweis ausführlich festgehalten. Diese Grafik hilft zum Verstehen: Zeichnet man ein großes Quadrat, bei dem Dreiecken die jede der Seiten aus Beweisidee: Aus einem gegebenen rechtwinkligem Dreieck ABC wird mit Hilfe des ein Dreieck PQB konstruiert, in welchem [BC] die Rolle einer Höhe spielt. Anschließend wird der
Einleitung Historische Grundlagen Beweis Satz des Pythagoras Pythagoras Beweis mit Scherung Quadratische Pyramide 2 Weiter Historische Grundlagen
Scherungsbeweis des Satzes von Pythagoras.Ziehe zuerst den grünen und danach den blauen Schieberegler. Beschreibe in eigenen Worten, was du passiert. Was haben das grüne, blaue
- Python Module Dir Function – Der_cert_to_pem_cert function of ssl module in Python
- Quais São Os Três Princípios De Economia De Movimentos?
- Pulmicort Flexhaler Side Effects: Common, Severe, Long Term
- Qual É A Diferença Entre Voz Ativa E Passiva Na Escrita?
- Public Holidays Syrien 1959 – Public Holidays Syrien 1975
- Qual O Rendimento Do Tijolo 6 Furos Por Metro Quadrado?
- Public Storage Dep.Prf.K Aktie (A3C7Sc
- Péréquation : Définition Simple Et Facile Du Dictionnaire
- Quais Os Melhores Livros Para Criancas De 9 Anos?
- Pöttinger Ladeprofi 3 G Kein Krone Strautmann Class Lely Fendt
- Qlikview-Kostenlos · Github Topics · Github
- Pulsex Statistieken: Markten, Handelsvolume En Trust Score