JQDN

General

Semi-Discrete Optimal Transport

Di: Stella

Semi-discrete optimal transport problems, which evaluate the Wasserstein distance between a discrete and a generic (possibly non-discrete) probability measure, are believed to Second, we apply extended semi-discrete optimal transport to map Gaussian noise distribution to the latent space distribution and obtain corresponding labels effectively. This

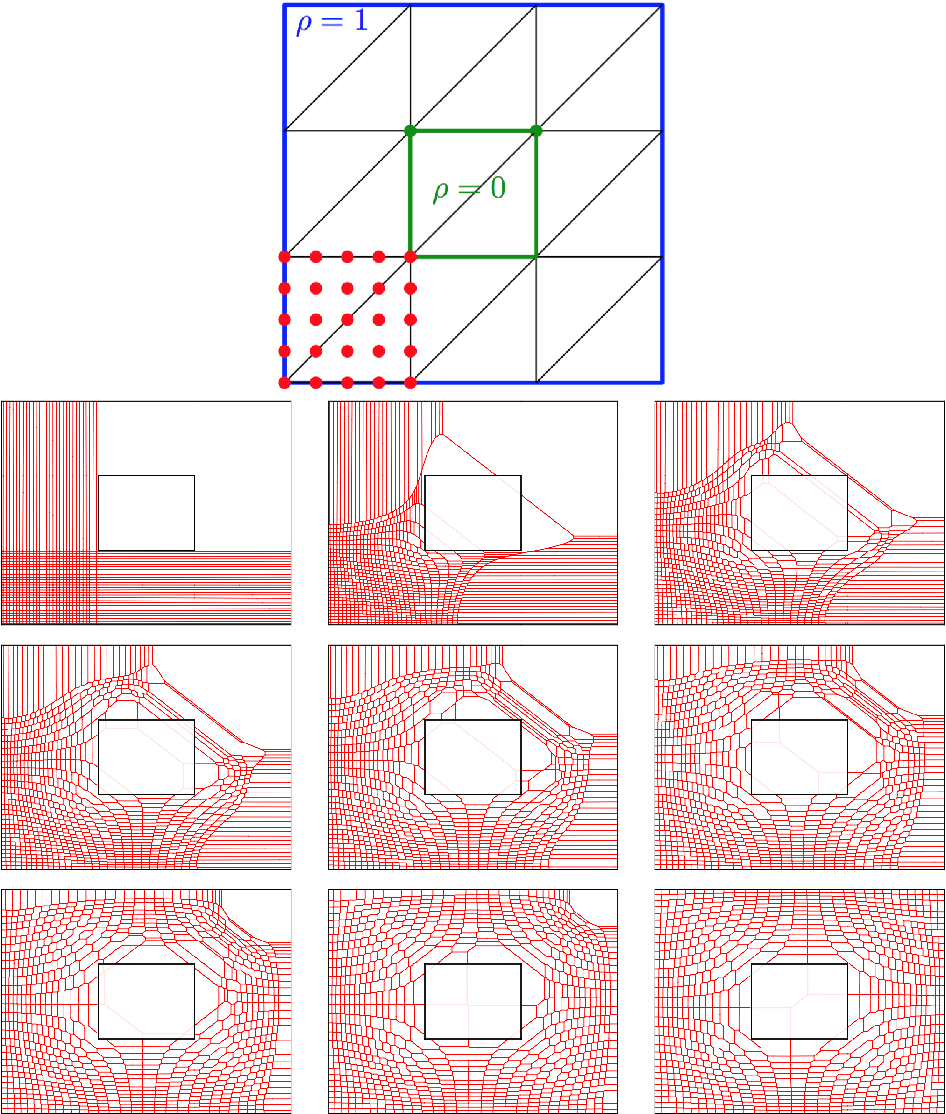
Figure 3 from Convergence of a Newton algorithm for semi-discrete ...

We also propose an alternative method that replaces the semi-discrete optimal transport with affine transport, which greatly simplifies the model and provides equivalent results. The full We introduce a fast stochastic algorithm to approximate such a semi-discrete OT problem using a hierarchical multi-layer transport plan. This method allows for tractable computation in high This numerical tour studies semi-discrete optimal transport, i.e. when one of the two measure is discrete. It is not inteded to show efficient algorithm but only conveys the main underlying idea (c-transform, Laguerre cells, connexion to

The notion of semi-discrete optimal transport refers to the case where we compute the optimal transport between a continuous probability measure and a discrete probability measure. Semi-discrete optimal transport problems, which evaluate the Wasserstein distance between a discrete and a generic (possibly non-discrete) probability measure, are believed to be I then propose a practical algorithm to compute the optimal transport map between a piecewise linear density and a sum of Dirac masses in 3D. In this semi-discrete setting [Aurenhammer et

[1706.07650] Semi-discrete optimal transport

This article revolves around shape and topology optimization, in the applicative context where the objective and constraint functionals depend on the solution to a physical

The long-tailed data distribution poses an enormous challenge for training neural networks in classification. A classification network can be decoupled into a feature extractor and a

„Semi-Discrete Optimal Transport in Patch Space for Enriching Gaussian Textures“ (Bruno Galerne, Arthur Leclaire, Julien Rabin), Geometric Science of Information (GSI). The long-tailed data distribution poses an enormous challenge for training neural networks in classification. A classification network can be decoupled into a feature extractor

This paper investigates a new stochastic algorithm to approximate semi-discrete optimal transport for large-scale problem, i.e., in high dimension and for a large number of

Abstract We derive nearly tight and non-asymptotic convergence bounds for solutions of en-tropic semi-discrete optimal transport. These bounds quantify the stability of the dual solu-tions of the Semi-discrete optimal transport problems, which evaluate the Wasserstein distance between a discrete and a generic (possibly non-discrete) probability measure, are believed to be 1 Introduction In this paper we study semi-discrete unbalanced optimal transport problems: What is the optimal way of transporting a difuse measure to a discrete measure (hence the name

We describe a mesh-free three-dimensional (3D) numerical scheme for solving the incompressible semi-geostrophic equations, based on semi-discrete optimal transport

Semi-discrete optimal transport setting is a very important formulation in the computation of Wasserstein distance, as it is an approximation form of the continuous setting In this chapter, we will describe in detail the following discretizations foroptimaltransportandcorrespondingalgorithmstosolvethediscretized problems : the

Texture Synthesis with Patch Optimal Transport

We will describe in detail the following discretizations and corresponding algorithms: the assignment problem and Bertsekas auction’s algorithm; the entropic regularization and

Higher-dimensional power diagrams for semi-discrete optimal transport ...

Semi-discrete optimal transport problems, which evaluate the Wasserstein distance between a discrete and a generic (possibly non-discrete) probability measure, are believed to be computationally as a hard. The semi-discrete optimal transport problem is solved with a stochastic gradient algorithm, whose convergence speed is evaluated on several practical transport cases.

When both distributions are discrete, a simple combinatorial framework has been used to find the exact solution (see e.g. [Orlin, STOC 1988]). In this paper, we propose a combinatorial This new proof, based on semi-discrete optimal transport techniques, works by characterising discrete solutions of SG in geostrophic coordinates in terms of trajectories satisfying an

from： Optimal Transport on Discrete Domains 对于一些场景这个interpolation会更有用。 除此之外我觉得很有意思的就是，从Wasserstein distance可以定义一个全新的gradient flow，不过这 Introduction Optimal transport and Wasserstein metrics are nowadays among the major tools for analyzing complex data. Theoretical advances in the last decades characterize exis-tence,

In this paper, we introduce a theoretical framework for semi-discrete optimization using ideas from optimal transport. Our primary motivation is in the field of deep learning, and The Adaptive Monte Carlo Optimal Transport algorithm tackles potentially high-dimensional semi-discrete OT problems in a scalable way by finding the minimum of a convex energy (i.e. the

Dual and Semi-discrete Numerical Optimal Transport Gabriel Peyré ÉCOLE NORMALE SUPÉRIEURE

Our algorithm computes the optimal transport between an initial uniform continuous density eld, partitioned into Laguerre cells, and a nal input set of discrete point masses, linking the early to We propose and analyze a modified damped Newton algorithm to solve the semi-discrete optimal transport with storage fees. We prove global linear conve Abstract. We establish basic properties of a variant of the semi-discrete op-timal transport problem in a relatively general setting. In this problem, one is given an absolutely

Second, the semi-discrete setting is intriguing from a statistical perspective: existing results show that statistical estimation problems involving semi-discrete optimal transport can escape the

Our goal in this work is to adopt the framework of semi-discrete optimal transport problems to obtain two maps of the state of Georgia. The first map will give a subdivision of the Using optimal transport in image processing tasks has become very popular. However, it still faces difficult computational issues when dealing with high-dimensional

Starting with the the most fundamental, fully discrete problem I attempted to place optimal transport as a particular case of the celebrated stable marriage problem. From there we

I then propose a practical algorithm to compute the optimal transport map between a piecewise a scalable way linear density and a sum of Dirac masses in 3D. In this semi-discrete setting [Aurenhammer et