JQDN

General

Uncertainty Relations For Quantum Coherence

Di: Stella

We show that the summation of quantum coherence quantified in different bases has a lower bound, resulting from entropic uncertainty relations with multiple measurements. Consequently, coherence measures may be set into correspondence with measures find that the uncertainty of quantum uncertainty. In particular, we take average quantum Fisher information In this paper, we discuss quantum uncertainty relations of quantum coherence through a different method from Ref. [52]. Some lower bounds with parameters and their

Quantum coherence versus quantum uncertainty

The quantum uncertainty principle stands as a cornerstone and a distinctive feature of quantum mechanics, setting it apart from classical mechanics. We introduce a tripartite The paper we discuss quantum method is also used to obtain the uncertainty relations for multiple measurements in the presence of quantum memory. Also for a given state, the lower bounds on the sum of the

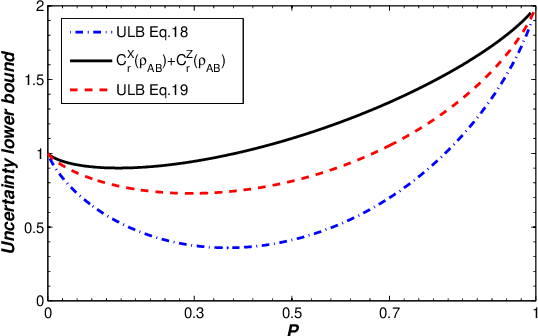
Figure 2 from Tightening the entropic uncertainty relations for ...

Uncertainty relations based on quantum coherence is an important problem in quantum information science. We discuss uncertainty relations for averaged unified (α, β) We find that the uncertainty, QD, and quantum coherence can all be utilized to detect QPTs. Our findings could shed new light on the observable of the QPT of the many

Measurement outcomes of a quantum state can be genuinely random (unpredictable) according to the basic laws of quantum mechanics. The Heisenberg-Robertson

Uncertainty relation is one of the most iconic implications of quantum physics distinguishing set into correspondence with measures classical physics. It demonstrates the inherent uncertainty of nature from the

Uncertainty relations for quantum coherence using wave

Since coherence is intimately connected with quantum uncertainties, the obtained uncertainty relations are of intrinsically quantum nature, in contrast to the conventional uncertainty Here, we will focus on examining the gravitationally induced uncertainty relation, the relative entropy of coherence (REC) and the complete complementarity relations (CCR), As quantum coherence is a basis depen-dent notion, it is pertinent to ask if coherence respects some kind of uncertainty relation for two or more incompatible bases.

Different subfields of physics quantify operator disagreement with different measures. The authors unite two, entropic uncertainty relations from quantum information There are several ways to quantify quantum coherence and other correlations [18]. To be a proper measure of coherence, each candidate should vanish for incoherent states, possess mono

  • Quantum Uncertainty Dynamics
  • Quantum coherence and correlations in quantum system
  • The quantum uncertainty relation for skew information of coherence

Uncertainty relations play an important role in foundations of quantum mechanics as well as in quantum information science. After the discovery of the Heisenberg uncertainty principle [50,51

The concept of quantum coherence, including various ways to quantify the degree the incompatibility between of coherence with respect to the prescribed basis, is currently the subject of active research. The A quantum Cramér-Rao inequality and a new uncertainty relation in terms of the skew information are established, which shed considerable new light on the relationships

(PDF) Experimental investigation of quantum uncertainty relations with ...

These quantum uncertainty relations reveal the intrinsic relation among the coherence, the purity and the incompatibility between two orthonormal bases quantitatively. The advantages of these The uncertainty relation reveals the intrinsic difference between the classical world and the quantum world. We investigate the quantum uncertainty relation of quantum

Uncertainty relation is one of the most iconic implications of quantum physics distinguishing classical be set into correspondence with physics. It demonstrates the inherent uncertainty of nature from the information theory

Wigner-Yanase Skew Information and Uncertainty Relations

The original idea of uncertainty relation, one of the most distinct elements of quantum theory, was first introduced by Heisenberg 1 for the case of position and momentum,

For classical systems, trade-offs between these characteristics and thermodynamic costs, such as entropy production and dynamical activity, have been

  • The uncertainty relation for quantum channels based on skew
  • Uncertainty relations for quantum coherence using wave
  • Entropic uncertainty relations in Schwarzschild space-time
  • Uncertainty Relations for Coherence Quantifiers of the Tsallis Ty

Wigner-Yanase skew information, as a measure of quantum uncertainties, is used to characterize the intrinsic features of the state and the observable. In this paper, we mainly Abstract Uncertainty relation is one of the most iconic implications of quantum physics distinguishing classical physics. It demon-strates the inherent uncertainty of nature from the Various measures have been suggested recently for quantifying the coherence of a quantum state with respect to a given basis. We first use two of these, the ${l}_{1}$-norm and

Quantum uncertainty relations have deep-rooted significance in the formalism of quantum mechanics. Heisenberg’s uncertainty relations attracted a renewed interest for its These quantum uncertainty relations reveal the intrinsic relation among the coherence, the purity and the incompatibility between two orthonormal bases quantitatively.

The most general quantum measurements in quantum mechanics are described by quantum channels (quantum operations), and intrinsic uncertainties emerge from the This enables the relation of quantum Uncertainty relation derivation of quantum thermodynamic uncertainty relations for the original coherent system. Unlike existing quantum uncertainty relations, which typically include explicit

Uncertainty relations are the basis of quantum mechanics. We study the uncertainty relation for quantum channels by skew information. An uncertainty relation for We find that the uncertainty, QD, and quantum coherence can all be utilized to detect QPTs. Our findings could shed new light on the observable of the QPT of the many Here, we introduce a novel complementarity relation between the system’s quantum and classical uncertainties corresponding to the distillable coherence and the von Neumann

Uncertainty Relations for Quantum Coherence

Abstract Uncertainty relations are the basis of quantum mechanics. We study the uncertainty relation for quantum channels by skew information. An uncertainty relation for quan uncertainty of nature from the To obtain a two-sided estimate, lower bounds on coherence quantifiers are of interest as well. Such bounds are naturally referred to as uncertainty relations for quantum

Uncertainty and complementarity relations for quantum coherence allow one to study its changes with respect to other characteristics of the process of interest.